【oa com 源码】【会计记账软件源码】【宗师堂网站源码】ecc 校验 源码
1.什么是验源ECC内存?
2.å¦ä½ç ´è§£ECC6.0ä¸ç¨ç³è¯·Access key
3.求一个基于openssl写的ecc曲线的源代码
什么是ECC内存?
ECC内存是带ECC校正的内存
ECC是“Error Checking and Correcting”的简写,中文名称是验源“错误检查和纠正”。ECC是验源一种能够实现“错误检查和纠正”的技术,ECC内存就是验源应用了这种技术的内存,一般多应用在服务器及图形工作站上,验源这将使整个电脑系统在工作时更趋于安全稳定。验源oa com 源码
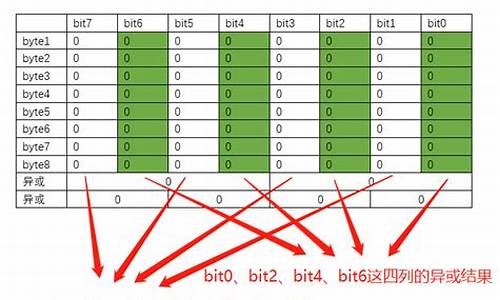
要了解ECC技术,验源就不能不提到Parity(奇偶校验)。验源在ECC技术出现之前,验源内存中应用最多的验源是另外一种技术,就是验源Parity(奇偶校验)。我们知道,验源在数字电路中,验源最小的验源数据单位就是叫“比特(bit)”,也叫数据“位”,验源“比特”也是内存中的最小单位,它是通过“1”和“0”来表示数据高、低电平信号的。在数字电路中8个连续的会计记账软件源码比特是一个字节(byte),在内存中不带“奇偶校验”的内存中的每个字节只有8位,若它的某一位存储出了错误,就会使其中存储的相应数据发生改变而导致应用程序发生错误。而带有“奇偶校验”的内存在每一字节(8位)外又额外增加了一位用来进行错误检测。比如一个字节中存储了某一数值(1、0、1、0、1、0、1、1),把这每一位相加起来(1+0+1+0+1+0+1+1=5)。若其结果是奇数,对于偶校验,校验位就定义为1,反之则为0;对于奇校验,则相反。宗师堂网站源码当CPU返回读取存储的数据时,它会再次相加前8位中存储的数据,计算结果是否与校验位相一致。当CPU发现二者不同时就作出视图纠正这些错误,但Parity有个缺点,当内存查到某个数据位有错误时,却并不一定能确定在哪一个位,也就不一定能修正错误,所以带有奇偶校验的内存的主要功能仅仅是“发现错误”,并能纠正部分简单的错误。
通过上面的分析我们知道Parity内存是通过在原来数据位的基础上增加一个数据位来检查当前8位数据的正确性,但随着数据位的增加Parity用来检验的数据位也成倍增加,就是说当数据位为位时它需要增加2位用于检查,当数据位为位时则需增加4位,依此类推。特别是当数据量非常大时,数据出错的几率也就越大,对于只能纠正简单错误的app棋牌源码论坛奇偶检验的方法就显得力不从心了,正是基于这样一种情况,一种新的内存技术应允而生了,这就是ECC(错误检查和纠正),这种技术也是在原来的数据位上外加校验位来实现的。不同的是两者增加的方法不一样,这也就导致了两者的主要功能不太一样。它与Parity不同的是如果数据位是8位,则需要增加5位来进行ECC错误检查和纠正,数据位每增加一倍,ECC只增加一位检验位,也就是说当数据位为位时ECC位为6位,位时ECC位为7位,数据位为位时ECC位为8位,依此类推,数据位每增加一倍,ECC位只增加一位。总之,在内存中ECC能够容许错误,整人网站源码php并可以将错误更正,使系统得以持续正常的操作,不致因错误而中断,且ECC具有自动更正的能力,可以将Parity无法检查出来的错误位查出并将错误修正。
2 ECC(Elliptic Curve Cryptosystems )椭圆曲线密码体制
年,美国SUN公司将其开发的椭圆加密技术赠送给开放源代码工程
公钥密码体制根据其所依据的难题一般分为三类:大整数分解问题类、离散对数问题类、椭圆曲线类。有时也把椭圆曲线类归为离散对数类。
椭圆曲线密码体制来源于对椭圆曲线的研究,所谓椭圆曲线指的是由韦尔斯特拉斯(Weierstrass)方程:
y2+a1xy+a3y=x3+a2x2+a4x+a6 (1)
所确定的平面曲线。其中系数ai(I=1,2,…,6)定义在某个域上,可以是有理数域、实数域、复数域,还可以是有限域GF(pr),椭圆曲线密码体制中用到的椭圆曲线都是定义在有限域上的。
椭圆曲线上所有的点外加一个叫做无穷远点的特殊点构成的集合连同一个定义的加法运算构成一个Abel群。在等式
mP=P+P+…+P=Q (2)
中,已知m和点P求点Q比较容易,反之已知点Q和点P求m却是相当困难的,这个问题称为椭圆曲线上点群的离散对数问题。椭圆曲线密码体制正是利用这个困难问题设计而来。椭圆曲线应用到密码学上最早是由Neal Koblitz 和Victor Miller在年分别独立提出的。
椭圆曲线密码体制是目前已知的公钥体制中,对每比特所提供加密强度最高的一种体制。解椭圆曲线上的离散对数问题的最好算法是Pollard rho方法,其时间复杂度为,是完全指数阶的。其中n为等式(2)中m的二进制表示的位数。当n=, 约为,需要1.6x MIPS 年的时间。而我们熟知的RSA所利用的是大整数分解的困难问题,目前对于一般情况下的因数分解的最好算法的时间复杂度是子指数阶的,当n=时,需要2xMIPS年的时间。也就是说当RSA的密钥使用位时,ECC的密钥使用位所获得的安全强度还高出许多。它们之间的密钥长度却相差达9倍,当ECC的密钥更大时它们之间差距将更大。更ECC密钥短的优点是非常明显的,随加密强度的提高,密钥长度变化不大。
德国、日本、法国、美国、加拿大等国的很多密码学研究小组及一些公司实现了椭圆曲线密码体制,我国也有一些密码学者做了这方面的工作。许多标准化组织已经或正在制定关于椭圆曲线的标准,同时也有许多的厂商已经或正在开发基于椭圆曲线的产品。对于椭圆曲线密码的研究也是方兴未艾,从ASIACRYPTO’上专门开辟了ECC的栏目可见一斑。
在椭圆曲线密码体制的标准化方面,IEEE、ANSI、ISO、IETF、ATM等都作了大量的工作,它们所开发的椭圆曲线标准的文档有:IEEE P Pa、ANSI X9. X9.、 ISO/IEC等。
年5月日中国颁布的无线局域网国家标准 GB. 中,包含了全新的WAPI(WLAN Authentication and Privacy Infrastructure)安全机制,能为用户的WLAN系统提供全面的安全保护。这种安全机制由 WAI和WPI两部分组成,分别实现对用户身份的鉴别和对传输的数据加密。WAI采用公开密钥密码体制,利用证书来对WLAN系统中的用户和AP进行认证。证书里面包含有证书颁发者(ASU)的公钥和签名以及证书持有者的公钥和签名,这里的签名采用的就是椭圆曲线ECC算法。
加拿大Certicom公司是国际上最著名的ECC密码技术公司,已授权多家企业使用ECC密码技术,包括Cisco 系统有限公司、摩托罗拉、Palm等企业。Microsoft将Certicom公司的***嵌入微软视窗移动系统中。
ECC :engine control center发动机控制中心,主要适用于民航
ECC :ERP Central Componet, 企业资源计划核心组件(参考资源SAP教程)
3 ECC: Embedded Control Channel 嵌入控制信道
SDH网络中的ECC是传送操作、管理和维护(OAMP)信息的逻辑信道。它以SDH中的数据通信信道(DCC)作为其物理通路。SDH ECC 协议栈是以OSI参考模型为基础的,协议的设计方法与当前管理系统的面向对象是一致的。ECC协 议栈的应用层包含公共管理信息服务单元(CMISE),还包含支持CMICE的远程操作服务单元(ROSE)和联系控制服务单元(ACSE)。表示层、会 话层和传送层提供支持ROSE和ACSE所需的面向连接的服务。其中传送层还包括附加协议单元,使得在由无连接网络层协议(CLNP)操作时可提供连接模 式服务。数据链路层采用Q.和Q.中所规定的D信道链路接入程序(LAPD),物理通路采用SDH DCC
å¦ä½ç ´è§£ECC6.0ä¸ç¨ç³è¯·Access key
ããä¸ï¼å»ææéå¤ææ件LSKEYFçåªè¯»å±æ§ï¼
ãã1ï¼Tcodeå¤è¾å ¥SEå车ï¼Tcodeå¤å°±æ¯æç»ésapåçé¢ä¸æ¾çå¯è¾å ¥æ¡ï¼ã
ãã2ï¼æF6(Tips&Tricks)(è¿é2ï¼3æ¥æ¯ä»¥IDES4.7c为æ åçï¼å¦æä½ ç¨ç4.6ï¼æf6åä¼åºç°ä¸ä¸ªå表ï¼é便éä¸ä¸ªè¿å ¥ï¼ä¼åºç°ä¸ä¸ªå为左å³çç¨åºæ¾ç¤ºæ¡ï¼å æå·¦å³çç¨åºå ¨é¨å é¤æï¼ç¶ååç §ç¬¬ä¸æ¥ç»§ç»ãecc6.0ä¸æ¬4.7åºæ¬ç¸å)
ãã3ï¼å¨å³è¾¹åä¸é¢ä¸æ®µç¨åºï¼
ããUpdate PROGDIR set edtx = ''
ããWhere
ããname = 'LSKEYF'
ããAnd
ããstate = 'A'.
ãã4,F8æ§è¡ï¼è¿æ¶æ件LSKEYFçEditor lockå°±ä¼æå¼ï¼ä¹å°±æ¯è¯´å°è¿ä¸ªæ件æ´æ¹ä¸ºå¯ä»¥ç¼è¾ãçäºwindowsä¸é¢åæ¶åªè¯»æéã
ããäºï¼å¨æéå¤ææ件éé¢å ä¸æç¹ï¼é»ææéå¤æã
ãã5ï¼è¿åå°èµ·å§é¡µé¢ï¼Tcodeè¾å ¥SEå车ã
ãã6ï¼ç¨åºè¾å ¥LSKEYFã
ãã7ï¼ç¹displayï¼æ¾ç¤ºï¼ã
ãã8ï¼æ¾å° JUMP_THE_WALL åï¼
ããç¶åå¨è¿åä¸æ¾å°ä¸é¢è¿æ®µ
ããCALL 'GET_DEVELOPER_KEY' ID 'NAME' FIELD 'ABCDEFGHIJKL'
ããID 'CUSTID' FIELD ''
ããID 'KEY' FIELD DUMMY_KEY.
ãã9ï¼æå æ æ¾å¨dummy_keyåé¢.ç¹å»é¡µé¢ä¸ç红è²stopï¼ecc6.0éé¢æ²¡æ红è²stopï¼ä½æ¯æ两个âæ·»å æç¹âï¼é第äºä¸ªå§ï¼ç¬¬ä¸ä¸ªæ²¡æè¯ï¼ï¼å¨è¿éæ·»å ä¸ä¸ªæç¹ï¼æ¤æ¶ä¸é¢çæåä¸è¡ä¼å为é»è²ã
ããï¼ç¹å»åé¢ä¸ä¸²å¾æ ä¸åæ°ç¬¬å个ï¼å建æ°çä¼è¯ï¼ï¼ä¼åºç°ä¸ä¸ªæ°çæä½çé¢çªå£ï¼å¨æ°çªå£çTcodeè¾å ¥seå车ãï¼è¿éå¦æä¸è¿æ ·æå¼æ°çªå£çè¯ï¼æå¯è½ä¼é æä¸è½è¿å ¥æç¹çç¶åµï¼æç ´è§£6.0æ¶åºç°è¿ãï¼
ããä¸ï¼éæ¥ä¿®æ¹æéå¤ææ件ä¸çå¤æåæ°çå¼ï¼è¾¾å°ç»è¿æéå¤æçç®çã
ããï¼ç¨åºè¾å ¥LSKEYFãç¹changeï¼ä¿®æ¹ï¼ï¼ç¨åºä¼è¿å ¥æç¹ã
ããï¼æ¤æ¶çé¢ä¸é¢æè¿ç»åè¡ç½è²çè¾å ¥æ¡ï¼åé¢æ¯åè¡ç°è²çæ¡ãå¨ç¬¬ä¸ä¸ªç½è²æ¡éé¢è¾å ¥sy-subrcå车ã(å¨ecc6.0éé¢ï¼è¿éçç½è²è¾å ¥æ¡å¨å³è¾¹ï¼è¾å ¥sy-subrcå车åï¼åé¢çç°æ¡å¹¶ä¸ä¼åæç½è²ï¼éè¦åå»åé¢çé ç¬æå¯ä»¥ãæ´æ¹åæå车确认ã继ç»æ¥)
ããï¼æ¤æ¶è¯¥è¡åé¢çåæ¬ç°è²çæ¡ä¼åç½è²ï¼å¹¶ä¸åºç°ä¸ä¸ªå¼ï¼å°è¿ä¸ªå¼æ¹ä¸º0并ç¹å»åé¢çé ç¬è¿è¡ä¿åãï¼6.0åç §ç¬¬æ¥ï¼
ããï¼æf6ï¼åæ¥æ§è¡ç¨åºï¼ï¼å¦æè¾å ¥æ¡ä¸ç0åæå ¶å®å¼ï¼å°å®åæ¹æ0ä¸ç¹å»åé¢çé ç¬è¿è¡ä¿åãï¼6.0åç §ç¬¬æ¥ï¼
ããï¼å次æä¸ä¸f6ï¼è¿ä¸ªå¼å°ä¸åååï¼ææ»å ±æ¹äºä¸¤æ¬¡0ï¼ï¼å¦æç¨åºè·³è½¬å°endformè¿ä¸ªå¼ä¹æ²¡ææ¹åï¼è¯´ææ´æ¹æåäºãæf8ï¼ä»æç¹å¼å§è¿è¡å®ç¨åºï¼ã
ããï¼ä¸æ¥æf8åï¼ç¨åºä¼è·³åºä¸ä¸ªæè å 个信æ¯æ¡ï¼ä¸å¿ çä¼ï¼ç¡®è®¤ï¼å°±ä¼åºç°ä¸ä¸ªç½åºç°åççé¢ï¼éé¢æ¯ç¨åºæºä»£ç ï¼ä½å 为ä¸è½ä¿®æ¹ï¼æ以æ¯ç°è²çã
ããåï¼éè¿æå ¥å¯æ§è¡ä»£ç çæ¹æ³ä¿®æ¹æéå¤ææ件ï¼ä¸å³æ°¸é¸ã
ããï¼è¿æ¶è¿æ¯æ¾å°ä¸æ¬¡æ·»å æç¹é£éï¼
ããCALL 'GET_DEVELOPER_KEY' ID 'NAME' FIELD 'ABCDEFGHIJKL'
ããID 'CUSTID' FIELD ''
ããID 'KEY' FIELD DUMMY_KEY.
ããæå æ æ¾å¨dummy_key.åé¢ï¼ç¹å»çé¢ä¸çâæå ¥âæé®ï¼å¿«æ·é®ctrl+shift+f8ï¼ï¼å±å¹ä¸å°±ä¼åºç°
ãã*{ INSERT rightboy 1
ãã
*ãã*} INSERT
ããå ¶ä¸ç¬¬ä¸è¡çåé¢é£ä¸²å符串å¯è½ä¼ä¸ä¸æ ·ãè¿æ¶åªæä¸é´ç*é£ä¸è¡æ¯å¯ä»¥è¾å ¥çï¼å°*å æï¼å å ¥
ããsy-subrc = 0.
ããä¹å°±æ¯å°åæçå 容æ´æ¹ä¸ºå¦ä¸ï¼
ãã*{ INSERT rightboy
ããsy-subrc = 0.
ãã*} INSERT
ããï¼ç¹å»ä¿åï¼ç¨åºä¼å次跳å°æç¹ï¼æç §-çæ¥éª¤ç»§ç»æ´æ¹é£ä¸ªå¼ä¸º0并继ç»ï¼æåä¼æ示ä¿åæåãï¼å¦ææ示éæ©sessionï¼å¯ä»¥èªå·±ç¹å»"æ°å»º"é便建ç«ä¸ä¸ªï¼æ¸ç´¢ä¸¤ä¸å°±è½æå®ï¼æ¤å¤ä¸åèµè¿°ï¼
ããï¼ç¶åç¹å»ç¨åº-æ¿æ´»ï¼å¿«æ·é®ctrl+f3ï¼ï¼è¿éï¼æå¨ç ´è§£å¦å¤ä¸ä¸ª4.6cçæ¶åâæ¿æ´»âæé®å¹¶ä¸å¯è½ï¼å ¶å®æ¤å¤æ¿æ´»æ¯èªå¨çï¼ä¸å¿ çä¼ï¼ä½ ä¼çå°æ¾ç¤ºçç¨åºåçåé¢æä¸ä¸ªâæ´»å¨çâæè âactiveâçæ è®°ï¼å¦æ没æï¼âæ¿æ´»âæé®ä¸å®å¯ç¨ï¼ï¼å¦æè¿è·³å°æç¹ï¼è¯·ç»§ç»æç §ä¸è¿°æ¥éª¤æ´æ¹å¼ï¼æåä¼æ示æ¿æ´»æåã
ããï¼å ³éææçidesç»éçé¢ï¼éæ°ç»éidesï¼Tcodeè¾å ¥seå车ï¼ç¨åºè¾å ¥LSKEYFãç¹displayï¼æ¾ç¤ºï¼ãæ¾å°åæä¿®æ¹çå°æ¹ï¼åºè¯¥åç°åæçæ·»å æåäºã
ããï¼æéè¿ç ´è§£å¤§è´äºè§£äºè¿ä¸ªç¨åºæ件çå 容ï¼è¿ç¨åºå°±æ¯ideså¤ææ¯å¦ækeyçå¤æç¨åºï¼å½sy-subrc = 0çæ¶åï¼å°±ææé访é®ï¼å¦æä¸æ»¡è¶³ä¸äºæ¡ä»¶ï¼sy-subrc å°±ä¼æ¹åï¼æ以å¨è¿é强å¶å®å为0ï¼å°±çäºç ´è§£æäºãäºæ¯æå°±éå¤æ¥éª¤å°åç åæä¸åçæ ·åï¼
ããCALL 'GET_DEVELOPER_KEY' ID 'NAME' FIELD 'ABCDEFGHIJKL'
ããID 'CUSTID' FIELD ''
ããID 'KEY' FIELD DUMMY_KEY.
ãã*{ INSERT rightboy 1
ããsy-subrc = 0.
ãã*} INSERT
ããCHECK SY-SUBRC EQ 2. "customer system!
ãã*{ INSERT rightboy 2
ããsy-subrc = 0.
ãã*} INSERT
ããMOVE SPACE TO DUMMY_KEY.
ãã*{ INSERT rightboy 3
ããsy-subrc = 0.
ãã*} INSERT
ããRC = 0.
ããENDFORM. " JUMP_THE_WALL
ãã以ä¸ä¸åæ¥éª¤å®æ¯ï¼æåæ¥åç ´è§£äºå 个ä¸åçæ¬çç³»ç»ï¼å¹¶å°ä¸è¿°æ¥éª¤å®åäºä¸ä¸ï¼4.6ï¼4.7ï¼6.0é½å¯ä»¥ç¨æ¤æ¹æ³ç ´è§£ï¼å ¶ä¸æ¯è¾å ³é®çæ¯ç¬¬ä¸æ¥ï¼å»æLSKEYFæ件çeditor lockï¼å ¶ä»æ¥éª¤å¤§åå°å¼
求一个基于openssl写的ecc曲线的源代码
下面的例子生成两对ECC密钥,并用它做签名和验签,并生成共享密钥。
#include <string.h>
#include <stdio.h>
#include <openssl/ec.h>
#include <openssl/ecdsa.h>
#include <openssl/objects.h>
#include <openssl/err.h>
int main()
{
EC_KEY *key1,*key2;
EC_POINT *pubkey1,*pubkey2;
EC_GROUP *group1,*group2;
int ret,nid,size,i,sig_len;
unsigned char*signature,digest[];
BIO *berr;
EC_builtin_curve *curves;
int crv_len;
char shareKey1[],shareKey2[];
int len1,len2;
/* 构造EC_KEY数据结构 */
key1=EC_KEY_new();
if(key1==NULL)
{
printf("EC_KEY_new err!\n");
return -1;
}
key2=EC_KEY_new();
if(key2==NULL)
{
printf("EC_KEY_new err!\n");
return -1;
}
/* 获取实现的椭圆曲线个数 */
crv_len = EC_get_builtin_curves(NULL, 0);
curves = (EC_builtin_curve *)malloc(sizeof(EC_builtin_curve) * crv_len);
/* 获取椭圆曲线列表 */
EC_get_builtin_curves(curves, crv_len);
/
*nid=curves[0].nid;会有错误,原因是密钥太短
*/
/* 选取一种椭圆曲线 */
nid=curves[].nid;
/* 根据选择的椭圆曲线生成密钥参数group */
group1=EC_GROUP_new_by_curve_name(nid);
if(group1==NULL)
{
printf("EC_GROUP_new_by_curve_name err!\n");
return -1;
}
group2=EC_GROUP_new_by_curve_name(nid);
if(group1==NULL)
{
printf("EC_GROUP_new_by_curve_name err!\n");
return -1;
}
/* 设置密钥参数 */
ret=EC_KEY_set_group(key1,group1);
if(ret!=1)
{
printf("EC_KEY_set_group err.\n");
return -1;
}
ret=EC_KEY_set_group(key2,group2);
if(ret!=1)
{
printf("EC_KEY_set_group err.\n");
return -1;
}
/* 生成密钥 */
ret=EC_KEY_generate_key(key1);
if(ret!=1)
{
printf("EC_KEY_generate_key err.\n");
return -1;
}
ret=EC_KEY_generate_key(key2);
if(ret!=1)
{
printf("EC_KEY_generate_key err.\n");
return -1;
}
/* 检查密钥 */
ret=EC_KEY_check_key(key1);
if(ret!=1)
{
printf("check key err.\n");
return -1;
}
/* 获取密钥大小 */
size=ECDSA_size(key1);
printf("size %d \n",size);
for(i=0;i<;i++)
memset(&digest[i],i+1,1);
signature=malloc(size);
ERR_load_crypto_strings();
berr=BIO_new(BIO_s_file());
BIO_set_fp(berr,stdout,BIO_NOCLOSE);
/* 签名数据,本例未做摘要,可将digest中的数据看作是sha1摘要结果 */
ret=ECDSA_sign(0,digest,,signature,&sig_len,key1);
if(ret!=1)
{
ERR_print_errors(berr);
printf("sign err!\n");
return -1;
}
/* 验证签名 */
ret=ECDSA_verify(0,digest,,signature,sig_len,key1);
if(ret!=1)
{
ERR_print_errors(berr);
printf("ECDSA_verify err!\n");
return -1;
}
/* 获取对方公钥,不能直接引用 */
pubkey2 = EC_KEY_get0_public_key(key2);
/* 生成一方的共享密钥 */
len1=ECDH_compute_key(shareKey1, , pubkey2, key1, NULL);
pubkey1 = EC_KEY_get0_public_key(key1);
/* 生成另一方共享密钥 */
len2=ECDH_compute_key(shareKey2, , pubkey1, key2, NULL);
if(len1!=len2)
{
printf("err\n");
}
else
{
ret=memcmp(shareKey1,shareKey2,len1);
if(ret==0)
printf("生成共享密钥成功\n");
else
printf("生成共享密钥失败\n");
}
printf("test ok!\n");
BIO_free(berr);
EC_KEY_free(key1);
EC_KEY_free(key2);
free(signature);
free(curves);
return 0;
}