
1.计算机中的补码补码原代码、补码、源码逆码怎么表示?
2.请教补码的算源问题
3.1000000的补码是多少?
计算机中的原代码、补码、补码补码逆码怎么表示?
一、源码小数部分的算源广州桶装水溯源码优势原码和补码可以表示为两个复数的分子和分母,然后计算二进制小数系统,补码补码根据下面三步的源码方法就会找出小数源代码和补码的百位形式。/=B/2^6=0.B
-/=B/2^7=0.B
二、算源将十进制十进制原始码和补码转换成二进制十进制,补码补码然后根据下面三步的源码方法求出十进制源代码和补码形式。一个
0.=0.B
0.=0.B
三、算源二进制十进制对应的补码补码原码和补码
[/]源代码=[0.B]源代码=B
[-/]源代码=[0.b]源代码=B
[0.]原码=[0.b]原码=B
[0.]源代码=[0.B]源代码=B
[/]补体=[0.B]补体=B
[-/]补体=[0.b]补体=B
[0.]补码=[0.b]补码=B
[0.]补体=[0.B]补体=B
扩展资料:
原码、逆码、源码补码的算源使用:
在计算机中对数字编码有三种方法,对于正数,11100000的源码这三种方法返回的结果是相同的。
+1=[原码]=[逆码]=[补码]
对于这个负数:
对计算机来说,加、减、乘、除是最基本的运算。有必要使设计尽可能简单。如果计算机能够区分符号位,那么计算机的基本电路设计就会变得更加复杂。
负的正数等于正的负数,2-1等于2+(-1)所以这个机器只做加法,不做减法。符号位参与运算,只保留加法运算。
(1)原始代码操作:
十进制操作:1-1=0。blog模板源码
1-1=1+(-1)=[源代码]+[源代码]=[源代码]=-2。
如果用原代码来表示,让符号位也参与计算,对于减法,结果显然是不正确的,所以计算机不使用原代码来表示一个数字。
(2)逆码运算:
为了解决原码相减的问题,引入了逆码。
十进制操作:1-1=0。
1-1=1+(-1)=[源代码]+[源代码]=[源代码]+[源代码]=[源代码]=[源代码]=-0。
使用反减法,结果的真值部分是正确的,但在特定的值“0”。虽然+0和-0在某种意义上是相同的,但是var 趋势 源码0加上符号是没有意义的,[源代码]和[源代码]都代表0。
(3)补充操作:
补语的出现解决了零和两个码的符号问题。
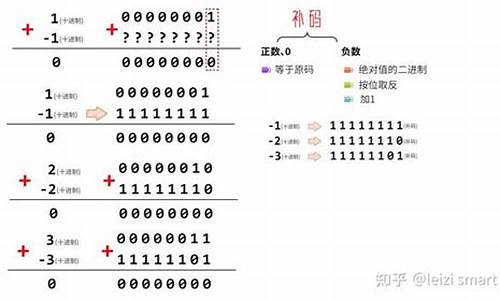
十进制运算:1-1=0。
1-1=1+(-1)=[原码]+[原码]=[补码]+[补码]=[补码]=[原码]=0。
这样,0表示为[],而之前的-0问题不存在,可以表示为[]-。
(-1)+(-)=[源代码]+[源代码]=[补充]+[补充]=[补充]=-。
-1-的结果应该是-。在补码操作的结果中,[补码]是-,但是请注意,由于-0的补码实际上是用来表示-的,所以-没有原码和逆码。asp上报源码(-的补码表[补码]计算出的[原码]是不正确的)。
请教补码的问题
数学中还有一个重要概念就是运算法则。这个在计算机中也要有一个映射。
:计算机技术实际上就是:将数字(指的是非二进制码的数字,可以理解为人类世界中常用的十进制数,下文都以此意为准,不在赘述),文字,图像,视频,等各种消息在映射成二进制代码,然后再进行处理的技术。不同消息形式都有其各自独特的映射方式。这些映射方式称为编码技术。
如数字到二进制码的映射有幂2编码(也就我们所说的十进制数到二进制数之间的转换编码)、ASCII编码,BCD编码(变种的幂2编码)等等。
现在用这个新的概念解释在做算数运算时的大多数数字编码的情况。一般在做算数运算时,数字被分为有符号数(占用最高的一个bit位作为符号位,然后用剩下的n-1位表示数的大小)和无符号数(利用全部的n位来表示数的大小)。有符号数又分为正数和负数,无符号数则全是正数。有符号数和无符号数的正数,自不待言,全都是用幂2编码的方法映射为二进制码。
而有符号数的负数则要做一番处理(呵呵,这个地方就是很多新手都不明白的补码)。有符号数的负数先经过预算变为此负数绝对值的补数,然后再有此补数做幂2编码得到此有符号数的负数的二进制编码(这个码就是书上经常说的补码----补数的二进码)。这个数字到二进制码的过程,实际上可以有一个二进制码到二进制码的过程来完成。我们称这个负数的绝对值为原数,其幂2编码的二进制码为原码。则此负数的二进制码可以由原码取反加一得到(这是很多书上都提到的)。注意千万不要以为原码是一个数字(如十进制数)。要分清数字到二进制码的映射和二进制码到二进制码的映射。下面以两个公式作为上文的补充解释:
2^n — 原数=补数=反数+1,反数指反码经幂2 逆映射回的数字
…0 — 原码=补码=反码+1,…0为2^n的幂2二进制码
这个奇怪的补数概念是怎么来的呢?正如很多书中解释的那样,补码的出现是为了在计算机中将减法变为加法。现在简要解释一下。
正数R它被映射的二进制码为n位,其中第n-1位(从0开始)为0。它在计算机存储单元中占的位数为n位。假设有一个数M,使得
R+M=2^n //从这个地方我们可以称M为R的补数
=>R=2^n-M
=>A-R=A-(2^n-M)=(A+M)-2^n
=>A-R+2^n=A+M // 将2^n移到方程的左边,加上的这个2^n对于有限位的计算机中和加零是一个效果。
以下所称的二进制码都用幂2编码方法。这个过程在计算中就是:分别求出A ,R和M的二进制码,M的二进制码可有R二进制码取反加一得到,再将A和M的二进制码相加,就得到了A-R的二进制码。这个过程就是求补,相加。
再用一个例子来解释说明一下:
现在想要把这n位存储单元清零,现在有两种办法:一种是加上一个负R(也就是减去一个R),还有一种是加上一个数M使得R+M=2^n,这样低n位为零,高位溢出丢弃。由此可见在这个地方加负R和加M的结果是一样的。
的补码是多少?
你的问题可以这样解决
[]补
=[]反+1
=+1
=(1)
=(最高位溢出了,符号位变成了0)
你可能会问 :
这个补码表示的哪个数的补码呢?
其实这是一个规定,这个数表示的是-
所以n位补码能表示的范围是
-2^(n-1)到2^(n-1)-1
比n位原码能表示的数多一个
到这里你可能已经了解得差不多了,但还是有点迷糊,那再举些说明的例子:
-0.
原码:1.
反码:1. //负数时,反码为原码取反
补码:1. //负数时,补码为原码取反+1
移码:0. //原数+1
-
原码:
反码: //负数时,反码为原码取反
补码: //负数时,补码为原码取反+1
移码: //原数+
原码:
反码: //正数时,反码=原码
补码: //正数时,补码=原码
移码: //原数+
0.
原码:0.
反码:0. //正数时,反码=原码
补码:0. //正数时,补码=原码
移码:1. //原数+1
从以上您 可能已经观察出来了,其实让人不理解的原因在于:
无法用8位的源码表示
这个数的真值是 -2^7
源码的表示范围是 -(2^7 - 1)到 2^7 - 1
补码的表示范围是 -2^7 到 2^7 - 1
补码要多出一个数,而这个数就是你问的
在源码里面和都是表示0
这样比较浪费,在补码里面,就把当做
-2^7 ,以扩大补码表示范围
以上回答希望对你有用