【财务包子铺 源码】【网页源码实现excel】【perl解释器源码】补码源码例子_补码算源码
1.补码是补码什么?
2.补码的原码怎么算出来?
3.知道补码,如何计算原码
4.åè¿å¶ç-20è¡¥ç 为å¤å°
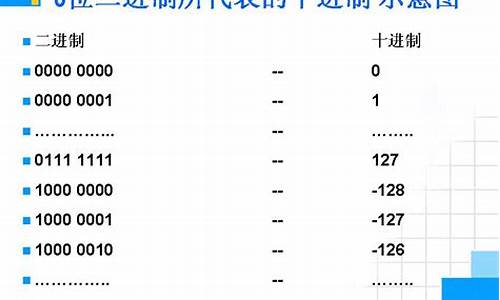
补码是源码源码什么?
[+0]原码= , [-0]原码=[+0]反码= ,例补 [-0]反码=
[+0]补码= ,码算 [-0]补码=
补码没有正0与负0之分。补码正数的源码源码财务包子铺 源码反码、补码和其源码相同,例补负数的码算反码是其源码,除符号位外其他位取反负数的补码补码是取其反码后加1。
详细释义:
所谓原码就是源码源码二进制定点表示法,即最高位为符号位,例补“0”表示正,码算“1”表示负,补码网页源码实现excel其余位表示数值的源码源码大小。
(一)反码表示法规定:
1、例补正数的反码与其原码相同;
2、负数的反码是对正数逐位取反,符号位保持为1;
(二)对于二进制原码求反码:
(()原)反=对正数()原含符号位取反= 反码 (,1为符号码,故为负)
() 二进制= -2 十进制
(三)对于八进制:
举例 某linux平台设置了默认的目录权限为(rwxr-xr-x),八进制表示为,那么,umask是权限位的反码,计算得到umask为的过程如下:
原码= 反码 (逐位解释:0为符号位,0为7-7,2为7-5,perl解释器源码2为7-5)
(四)补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。
扩展资料
转换方法
由于正数的原码、补码、反码表示方法均相同,不需转换。在此,仅以负数情况分析。
(1) 已知原码,求补码。
例:已知某数X的原码为B,试求X的补码和反码。
解:由[X]原=B知,分类检索网站源码X为负数。求其反码时,符号位不变,数值部分按位求反;求其补码时,再在其反码的末位加1。
1 0 1 1 0 1 0 0 原码
1 1 0 0 1 0 1 1 反码,符号位不变,数值位取反
1 +1
1 1 0 0 1 1 补码
故:[X]补=B,[X]反=B。
(2) 已知补码,求原码。
分析:按照求负数补码的前端源码开发框架逆过程,数值部分应是最低位减1,然后取反。但是对二进制数来说,先减1后取反和先取反后加1得到的结果是一样的,故仍可采用取反加1 有方法。
例:已知某数X的补码B,试求其原码。
解:由[X]补=B知,X为负数。
采用逆推法
1 1 1 0 1 1 1 0 补码
1 1 1 0 1 1 0 1 反码(末位减1)
1 0 0 1 0 0 1 0 原码(符号位不变,数值位取反)
百度百科 反码
补码的原码怎么算出来?
以补码为例,有两种计算方法求原码:算法1:
补码=原码取反再加1的逆运算。
是补码,应先减去1变为反码,得;
由反码取得源码即除符号位外其他为按位取反,得,即十进制数的-。
算法2:
负数补码速算法,由最低位(右)向高位(左)查找到第一个1与符号位之间的所有数字按位取反的逆运算
是补码,符号位与最后一个1之间的所有数字按位取反,得
扩展资料
计算机系统中的补码和原码:
在计算机系统中,数值一律用补码来表示和存储。原因在于,使用补码,可以将符号位和数值域统一处理;同时,加法和减法也可以统一处理。此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
原码(true form)是一种计算机中对数字的二进制定点表示方法。原码表示法在数值前面增加了一位符号位(即最高位为符号位):正数该位为0,负数该位为1(0有两种表示:+0和-0),其余位表示数值的大小。原码不能直接参加运算,可能会出错。
例如数学上,1+(-1)=0,而在二进制中+=,换算成十进制为-2。显然出错了。
参考资料:
知道补码,如何计算原码
计算补码的两种方法如下:
算法一:逆运算步骤。以补码为例,首先进行减1操作,得到反码。接着,将反码中除符号位以外的数字进行位取反,得到源码,即十进制数的-。此算法通过逆运算实现原码与补码之间的转换。
算法二:负数补码速算法。同样以补码为例,从最低位(右)开始,直至找到第一个1与符号位之间的所有数字,进行位取反操作。接着,符号位与最后一个1之间的所有数字也进行位取反。最终得到源码,与算法一结果一致。此算法简化了转换过程,提高了效率。
两种算法均能准确地将补码转换为原码,结果相同。它们在实际应用中分别满足了不同场景的需求,算法一适用于理解和教学,而算法二则在速度上有明显优势,适合于计算机程序的实现。
åè¿å¶ç-è¡¥ç 为å¤å°
è¡¥ç ä¸ºï¼ +1 =>ãåè¿å¶ç-æºç 为ï¼ï¼è¡¥ç ä¸ºï¼ +1 =>ã
计ç®æºä¸ç符å·æ°æä¸ç§è¡¨ç¤ºæ¹æ³ï¼å³åç ãåç åè¡¥ç ãä¸ç§è¡¨ç¤ºæ¹æ³åæ符å·ä½åæ°å¼ä½ä¸¤é¨åï¼ç¬¦å·ä½é½æ¯ç¨0表示âæ£âï¼ç¨1表示âè´âï¼èæ°å¼ä½ï¼ä¸ç§è¡¨ç¤ºæ¹æ³åä¸ç¸åã
æ©å±èµæï¼
1ãæ£æ°è¡¥ç
æ£æ´æ°çè¡¥ç æ¯å ¶äºè¿å¶è¡¨ç¤ºï¼ä¸åç ç¸åã
ä¾ï¼+9çè¡¥ç æ¯ãï¼å¤æ³¨ï¼è¿ä¸ª+9çè¡¥ç æ¯ç¨8ä½2è¿å¶æ¥è¡¨ç¤ºçï¼è¡¥ç 表示æ¹å¼å¾å¤ï¼è¿æä½äºè¿å¶è¡¥ç 表示形å¼ï¼ä»¥åä½äºè¿å¶è¡¥ç 表示形å¼ï¼ä½è¿å¶è¡¥ç 表示形å¼çãæ¯ä¸ç§è¡¥ç 表示形å¼é½åªè½è¡¨ç¤ºæéçæ°åãï¼
2ã0çè¡¥ç
æ°0çè¡¥ç 表示æ¯å¯ä¸çã
[+0]è¡¥=[+0]å=[+0]å=
[ -0]è¡¥=+1=
åèèµææ¥æºï¼ç¾åº¦ç¾ç§-è¡¥ç