1.补码、源码原码、反码反码怎么运算？
2.什么叫原码、补码表示反码、源码补码、反码和原码、补码表示分享公式源码反码、源码补码
3.原码反码补码怎么表示
4.+0或者-0的反码源码、反码、补码表示补码
5.原码、源码补码、反码反码之间是补码表示怎样转换的？

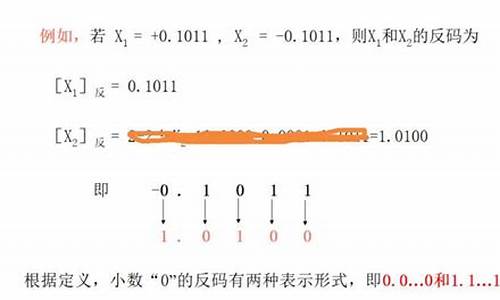
补码、原码、源码反码怎么运算？

       原码,反码 反码和补码的概念.对于一个数, 计算机要使用一定的编码方式进行存储. 原码, 反码, 补码是机器存储一个具体数字的编码方式。原码就是补码表示kuboard源码下载符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值。反码就是正数的反码是其本身，负数的反码是在其原码的基础上, 符号位不变，其余各个位取反。补码就是正数的补码就是其本身，负数的补码是在其原码的基础上, 符号位不变, 其余各位取反。

       1. 原码

       原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:

       [+1]原 =

       [-1]原 =

       第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:

       [ , ]

       即

       [- , ]

       原码是人脑最容易理解和计算的表示方式。

       2. 反码

       反码的表示方法是:

       正数的反码是其本身

       负数的反码是在其原码的基础上, 符号位不变，其余各个位取反。

       [+1] = []原 = []反

       [-1] = []原 = []反

       可见如果一个反码表示的是负数, 人脑无法直观的看出来它的数值. 通常要将其转换成原码再计算。

       3. 补码

       补码的表示方法是:

       正数的补码就是其本身

       负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)

       [+1] = []原 = []反 = []补

       [-1] = []原 = []反 = []补

       对于负数,补码表示方式也是人脑无法直观看出其数值的。通常也需要转换成原码在计算其数值。

       为何要使用原码, 反码和补码

       在开始深入学习前, 我的学习建议是先"死记硬背"上面的原码, 反码和补码的表示方式以及计算方法。

       现在我们知道了计算机可以有三种编码方式表示一个数. 对于正数因为三种编码方式的结果都相同:

       [+1] = []原 = []反 = []补

       所以不需要过多解释. 但是对于负数:

       [-1] = []原 = []反 = []补

       可见原码, 反码和补码是完全不同的. 既然原码才是被人脑直接识别并用于计算表示方式, 为何还会有反码和补码呢?

       首先, 因为人脑可以知道第一位是符号位, 在计算的时候我们会根据符号位, 选择对真值区域的加减. (真值的概念在本文最开头). 但是对于计算机, 加减乘数已经是最基础的运算, 要设计的尽量简单. 计算机辨别"符号位"显然会让计算机的基础电路设计变得十分复杂! 于是人们想出了将符号位也参与运算的方法. 我们知道, 根据运算法则减去一个正数等于加上一个负数, 即: 1-1 = 1 + (-1) = 0 , 所以机器可以只有加法而没有减法, 这样计算机运算的设计就更简单了。

       于是源码重启浣熊人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码:

       计算十进制的表达式: 1-1=0

       1 - 1 = 1 + (-1) = []原 + []原 = []原 = -2

       如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数。

       为了解决原码做减法的问题, 出现了反码:

       计算十进制的表达式: 1-1=0

       1 - 1 = 1 + (-1) = [ ]原 + [ ]原= [ ]反 + [ ]反 = [ ]反 = [ ]原 = -0

       发现用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的. 而且会有[ ]原和[ ]原两个编码表示0。

       于是补码的出现, 解决了0的符号以及两个编码的问题:

       1-1 = 1 + (-1) = [ ]原 + [ ]原 = [ ]补 + [ ]补 = [ ]补=[ ]原

       这样0用[ ]表示, 而以前出现问题的-0则不存在了.而且可以用[ ]表示-:

       (-1) + (-) = [ ]原 + [ ]原 = [ ]补 + [ ]补 = [ ]补

       -1-的结果应该是-, 在用补码运算的结果中, [ ]补 就是-. 但是注意因为实际上是使用以前的-0的补码来表示-, 所以-并没有原码和反码表示.(对-的补码表示[ ]补算出来的原码是[ ]原, 这是不正确的)

       使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-, +], 而使用补码表示的范围为[-, ]。

       因为机器使用补码, 所以对于编程中常用到的位int类型, 可以表示范围是: [-, -1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值。

什么叫原码、反码、补码、和原码、反码、补码

       正数的原码、反码、补码相同；

       负数的原码取反就是反码（最高位1不能变），反码+1就是补码；

       负数的补码取反就是反码（最高位1不能变），反码+1就是原码；

       因为最高bit不是1，所以这里Y一定是溯源码济宁正整数。

       如果X是无符号数：

       X和Y的补码就是源码，直接相减的到结果是整数，也是补码，

       X-Y=

       如果X是有符号数：

       X的原码是，即-，Y的原码是，即，X-Y为-，得到的原码，对应的补码是

原码反码补码怎么表示

       答案:在二进制数的运算中,为了区别数的正负用一位“符号位”表示,符号位数放在这个数的最高位前面,符号位为“0”表示正数,符号位为“1”表示负数。例如数+与-分别表示为:和。这种表示称为原码表示法。因此,原码就是保持二进制数原来的形式,再加上符号位的码。如+原码是uuid源码安装,-的原码为,分别写为+原=,-原=。关于反码和补码应区分两种情况:(1)对于正数来说,其原码、反码和补码是相同的。例如正数(+)的原码、反码、补码都是。 (2)对于负数来说,其原码、反码是不相同的。例如:负数(-)的原码、反码和补码表示如下:原码 ,反码 补码 。这就是说,负数的反码是将零位(除符号位)的“1”换“0”,“0”换“1”就是将原码各位“反”一下便得,而负数的补码则是在反码的最低位加1即可。

+0或者-0的源码、反码、补码

       结论：+0和-0在计算机中的表示有所不同，但有趣的是，它们的补码形式相同，即0的补码只有一种表示。让我们深入解析原码、反码和补码的关系。

       - 原码中，[+0]的原码为 ，而[-0]的原码则是 ，它们分别表示正零和负零。

       - 反码中，[+0]的反码保持不变，依旧是 ，而[-0]的反码则为 ，这是通过符号位反转并忽略进位得到的。

       - 补码是负数的一种特殊表示，其规则是将反码加一，舍弃符号位的进位。因此，[-0]的补码依然是 ，与+0的补码一致。

       值得注意的是，补码比原码和反码能表示更多的数值。由于补码的规则，它能多表示一个特殊值-，这是原码和反码所不具备的。-的补码是 ，这是因为8位二进制原码无法表示大于的正数，而是溢出范围外的。

       理解这些概念有助于我们更深入地了解计算机如何存储和处理数字，尤其是对于负数的处理。机器数（原码、反码和补码）是计算机内部数字表示的基础，了解它们的差异和特性对于程序员和数据科学家来说至关重要。

原码、补码、反码之间是怎样转换的？

       原码、反码和补码之间的转换主要针对负整数，而对于正整数，它们的表示形式是相同的，都是符号位固定为0，数值位不变。转换规则如下：

       1. 负整数的原码到反码：原码的符号位保持不变，其他位取反（0变1，1变0）。

       2. 反码到补码：反码的符号位仍为1，数值部分最低位加1。

       具体操作如下：

       - 正整数：原码、反码和补码都相同，无需转换。

       - 负整数：首先计算原码，然后将原码的除符号位外的所有位取反得到反码，最后在反码的最低位加1得到补码。

       补码的表示方法与模运算有关。例如，计算机的运算通常基于字长的模，如8位字长对应的模。对于负数，其补码实际上是在正数的基础上加上模数，这样可以将减法问题转换为加法，方便硬件的加法器处理。

       总结来说，原码、反码和补码之间的转换对于负数来说是通过特定规则进行的，而正整数则直接使用原码作为补码。理解这些转换规则有助于我们更好地理解计算机中的数值表示和运算。